Table of Contents

• DataSet
• Compreendendo o problema
  • Informações de atributo
• Configuração Inicial
• Exploração
• Limpeza
• Discretização
• Visualização
• Quais atributos tem relação?
• Distribuição de algumas colunas do DataSet
• Calculo de Insuficiência Cardíaca
• Inicio de Treinamento de Modelos
  • Separação de Dados
• Desision Tree
  • Medidas de seleção de atributo
• Randon Fores
• Logistic Regression
• GaussianNB
  • Calculo do algoritmo
• Matriz Confusão
• Cross-Validation
• Curva ROC
• Insigths

Projeto GitHub

heart-failure-prediction

Olá, meu nome é Patrick Piccini, e seja bem vindo a mais um projeto de Data Science.

O que iremos ver nesse Projeto:

• 📚 DataSet
• 🧠 Compreendendo o problema
• ⛏ Analise Exploratoria de Dados
• 🎲 Manipulação de dados
• 📊 Visualização de dados
• 🧮 Algoritmos de Classificação
• 😱 Insigths

DataSet

Heart Failure Prediction Dataset - Kaggle

Compreendendo o problema

As doenças cardiovasculares (DCVs) são a causa número 1 de morte em todo o mundo, levando cerca de 17,9 milhões de vidas a cada ano, o que representa 31% de todas as mortes em todo o mundo. Quatro das mortes por 5CVD são devido a ataques cardíacos e derrames, e um terço dessas mortes ocorre prematuramente em pessoas com menos de 70 anos de idade. A insuficiência cardíaca é um evento comum causado por DCV e este conjunto de dados contém 11 características que podem ser usadas para prever uma possível doença cardíaca.

Pessoas com doença cardiovascular ou com alto risco cardiovascular (devido à presença de um ou mais fatores de risco, como hipertensão, diabetes, hiperlipidemia ou doença já estabelecida) precisam de detecção e gerenciamento precoces, onde um modelo de aprendizado de máquina pode ser de grande ajuda.

Informações de atributo

• Age: idade do paciente [anos]
• Sex: sexo do paciente [M: Masculino, F: Feminino]
• ChestPainType: tipo de dor no peito [TA: Angina Típica, ATA: Angina Atípica, NAP: Dor Não Anginosa, ASY: Assintomática]
• RestingBP: pressão arterial de repouso [mm Hg]
• Cholesterol: colesterol sérico [mm/dl]
• FastingBS: glicemia em jejum [1: se FastingBS > 120 mg/dl, 0: caso contrário]
• RestingECG: resultados do eletrocardiograma de repouso [Normal: normal, ST: com anormalidade da onda ST-T (inversões da onda T e/ou elevação ou depressão do ST > 0,05 mV), HVE: mostrando provável ou definitiva hipertrofia ventricular esquerda pelos critérios de Estes]
• MaxHR: frequência cardíaca máxima alcançada [Valor numérico entre 60 e 202]
• **ExerciseAngina: angina induzida por exercício [S: Sim, N: Não]
• Oldpeak: pico antigo = ST [Valor numérico medido em depressão]
• ST_Slope: inclinação do segmento ST do exercício de pico [Up: upsloping, Flat: flat, Down: downsloping]
• HeartDisease: classe de saída [1: doença cardíaca, 0: normal]

Configuração Inicial

import numpy as np 
import pandas as pd
import seaborn as sns
from sklearn import tree
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score, classification_report, confusion_matrix, ConfusionMatrixDisplay, RocCurveDisplay, precision_recall_fscore_support

heart_df = pd.read_csv('./dataset/heart.csv', sep=',')

• Iremos renomear o nome das colunas para Português, onde facilitará na hora do entendimento da informação dos dados.

columns = {
    'Age': 'Idade',
    'Sex': 'Sexo', 
    'ChestPainType': 'Tipo_Dor_Peito', 
    'RestingBP': 'RepousoPA', 
    'Cholesterol': 'Colesterol', 
    'FastingBS': 'FastingBS',
    'RestingECG': 'RestingECG', 
    'MaxHR': 'Frequencia_Cardiaca_Max', 
    'ExerciseAngina': 'Exercicio_Angina', 
    'Oldpeak': 'Pico_Antigo', 
    'ST_Slope': 'ST_Slope',
    'HeartDisease': 'Doenca_Cardiaca'
}

heart_df = heart_df.rename(columns=columns)
heart_df.head(5)

Exploração

• Verificaremos a quantidade de colunas e linhas existentes no DataSet.

print('Colunas: %s' % heart_df.shape[1])
print('Linhas: %s' % heart_df.shape[0])

• Colunas: 12
• Linhas: 918

Com o comando “describe”, iremos obter um resumo de estatísticas descritivas do DataFrame. Isso inclui média, contagem, desvio padrão, percentis e valores mín.-máx. de todos os recursos. Com o ".T” apenas iremos rotacionar o resultado do “describe”.

heart_df.describe().T

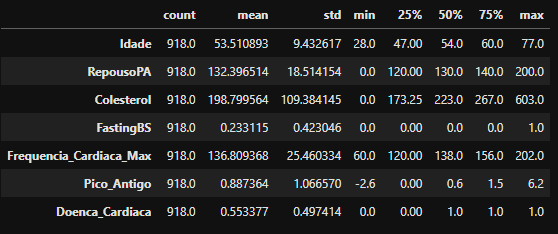
Abaixo veremos mais algumas informações referentes a cada coluna do DataFrame.

heart_df.info()

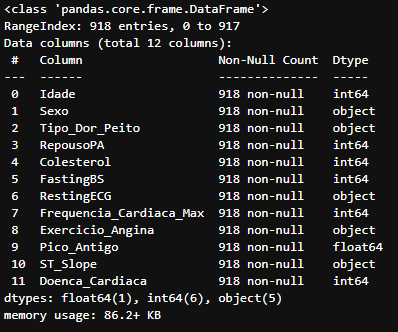
Limpeza

Percebemos que não existem valores NaN em nosso DataSet, porém, existem muitos valores do colesterol igual a 0 (Zero). Visto isso, para não perdermos informações, substituiremos os valores de 0 (Zero) para um valor “Saudável” sendo 130.

Para termos uma visualização de como irá influenciar a limpeza de dados, iremos salvar os dois estados da coluna colesterol, para posteriormente plotarmos um grafico.

print(heart_df.notna().value_counts())

colesterol_0 = heart_df.Colesterol
heart_df.Colesterol = heart_df.Colesterol.replace(0, 130)
colesterol_no_0 = heart_df.Colesterol

Discretização

Formar conjuntos de idade para classificação.

print('Idade máxima: ',heart_df.Idade.max())
print('Idade MINIMA: ',heart_df.Idade.min())

• Idade máxima: 77
• Idade MINIMA: 28

bins = [0,12,20,60,100]
labels = ['crianca','adolecente','adulto','idoso']
conjuto_idade = pd.cut(heart_df['Idade'].to_numpy(), bins=bins, labels=labels)

heart_df['conjunto_idade'] = conjuto_idade

heart_df.head(3)

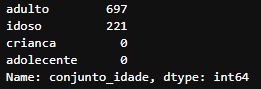
heart_df.conjunto_idade.value_counts()

Visualização

Nesse passo da AED iremos plotar alguns gráficos onde consiguiremos ter uma análise das informações um pouco mais dinâmica, e com isso conseguiremos criar alguns insigths de nossas informações

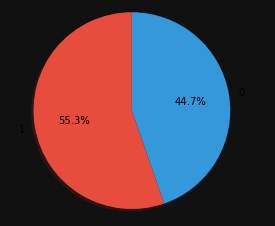
• Iremos calcular a porcentagem de casos de pessoas com Insuficiência Cardíacas e sem Insuficiência Cardía

print("paciente com Insuficiência Cardíacas:", heart_df.query('Doenca_Cardiaca == 1').shape[0])
print("paciente sem Insuficiência Cardíaca:", heart_df.query('Doenca_Cardiaca == 0').shape[0])

labels = [1,0]
sizes = heart_df['Doenca_Cardiaca'].value_counts()
explode = (0, 0.1, 0, 0)

fig1, ax1 = plt.subplots()
ax1.pie(sizes, labels=labels, autopct='%1.1f%%',shadow=True, startangle=90 ,colors=['#E74C3C','#3498DB'])
ax1.axis('equal')  # Equal aspect ratio ensures that pie is drawn as a circle.
plt.show()

• paciente com Insuficiência Cardíacas: 508
• paciente sem Insuficiência Cardíaca: 410

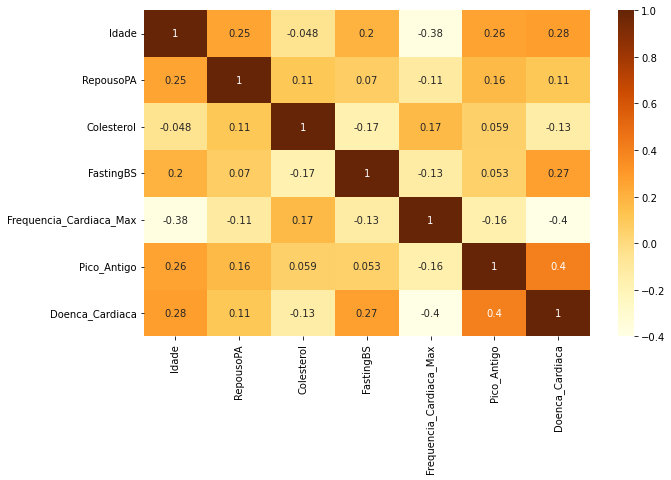
Quais atributos tem relação?

Através de uma HeatMap (Mapa de calor), verificaremos quais as relações que os atributos tem com a coluna alvo, que no nosso caso é a _DoencaCardiaca

Podemos ver que a Doença Cardíaca tem grande relação com uma “Pico_Antigo” alta e tambem uma relação com “Idade”. Há uma relação boa com “",“FastingBS” e “RepousoPA”.

plt.figure(figsize=(10,6))

sns.heatmap(heart_df.corr(), annot=True, cmap ="RdYlBu")
plt.show()

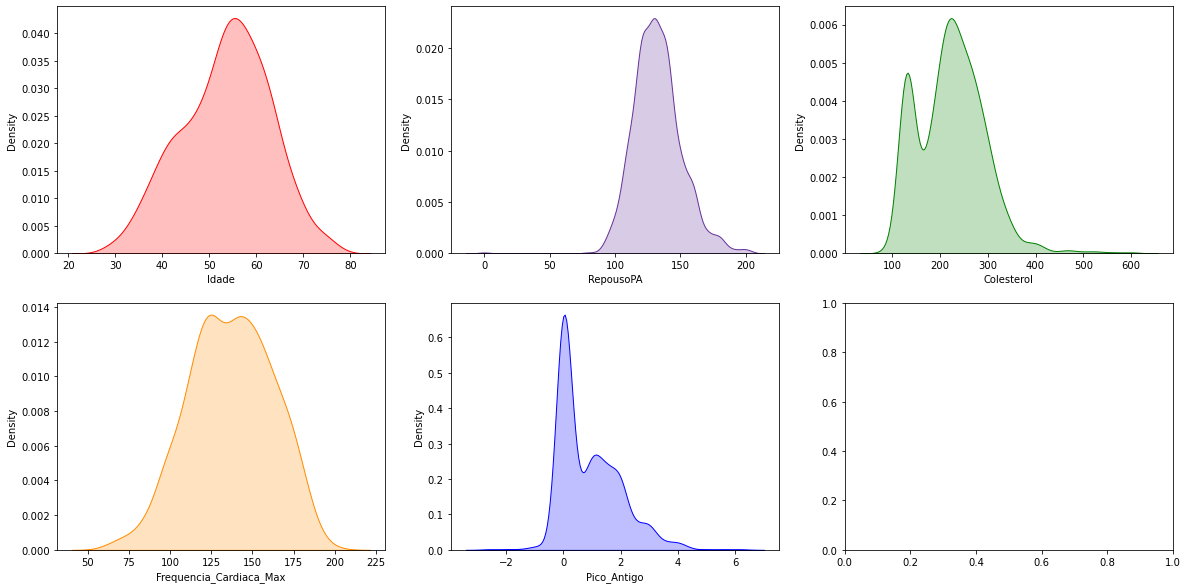
Distribuição de algumas colunas do DataSet

Vendo os gráficos plotados, conseguimos perceber o volume de informações sobre determinado valor, de acordo com sua coluna.

Uma coisa que podemos notar no gráfico do colesterol, é que há uma grande quantidade de dados com o valor 0 ou negativo. Fazendo um pesquisa rápida na internet, entende-se que existe certo consenso de que valores do LDL-Colesterol (¨colesterol ruim”) menores que 40 mg/dl no sangue são considerados baixos, entretanto, estudos recentes não demonstraram efeitos colaterais graves mesmo quando esse valor foi reduzido até 25mg/dl. Sendo assim, esses dados zeros ou negativos certamente estão errados, e com isso, podemos tratá-los como Outliers.

fig, axes = plt.subplots(2, 3, figsize=(20, 10))
sns.kdeplot(heart_df['Idade'], ax = axes[0, 0] ,shade=True, color='r')
sns.kdeplot(heart_df['RepousoPA'], ax = axes[0, 1], shade=True, color='rebeccapurple')
sns.kdeplot(heart_df['Colesterol'], ax = axes[0, 2], shade=True, color='g')
sns.kdeplot(heart_df['Frequencia_Cardiaca_Max'], ax = axes[1, 0], shade=True, color='darkorange')
sns.kdeplot(heart_df['Pico_Antigo'], ax = axes[1, 1], shade=True, color='blue')
plt.show()

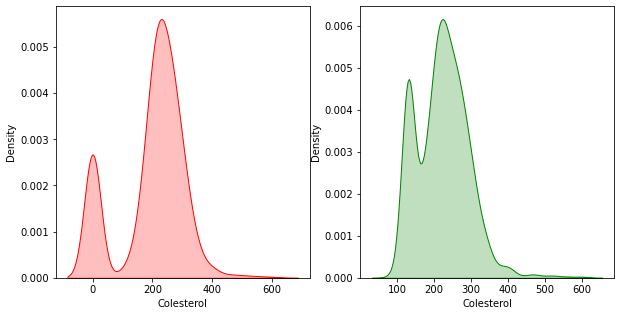
Antes de continuarmos, vamos ver a diferença dos gráficos referente ao Colesterol, visto que tivemos alguns valores modificados no passo de Limpeza dos dados. Apenas relembrando, trocamos os valores 0 do colesterol, para um valor “saudável”, sendo esse 130.

fig, axes = plt.subplots(1, 2, figsize=(10, 5))
sns.kdeplot(colesterol_0, ax = axes[0], shade=True, color='r')
sns.kdeplot(colesterol_no_0, ax = axes[1], shade=True, color='g')
plt.show()

Calculo de Insuficiência Cardíaca

fig, axes = plt.subplots(3, 2, figsize=(20, 10))

sns.countplot(x="Sexo", hue="Doenca_Cardiaca", data=heart_df, ax=axes[0, 0] ,palette=['#3498DB','#E74C3C'])
sns.countplot(x="Tipo_Dor_Peito", hue="Doenca_Cardiaca", data=heart_df, ax=axes[0, 1] ,palette=['#3498DB','#E74C3C'])
sns.countplot(x="RestingECG", hue="Doenca_Cardiaca", data=heart_df, ax=axes[1, 0] ,palette=['#3498DB','#E74C3C'])
sns.countplot(x="ST_Slope", hue="Doenca_Cardiaca", data=heart_df, ax=axes[1, 1] ,palette=['#3498DB','#E74C3C'])
sns.countplot(x="conjunto_idade", hue="Doenca_Cardiaca", data=heart_df, ax=axes[2, 0] ,palette=['#3498DB','#E74C3C'])
plt.show()

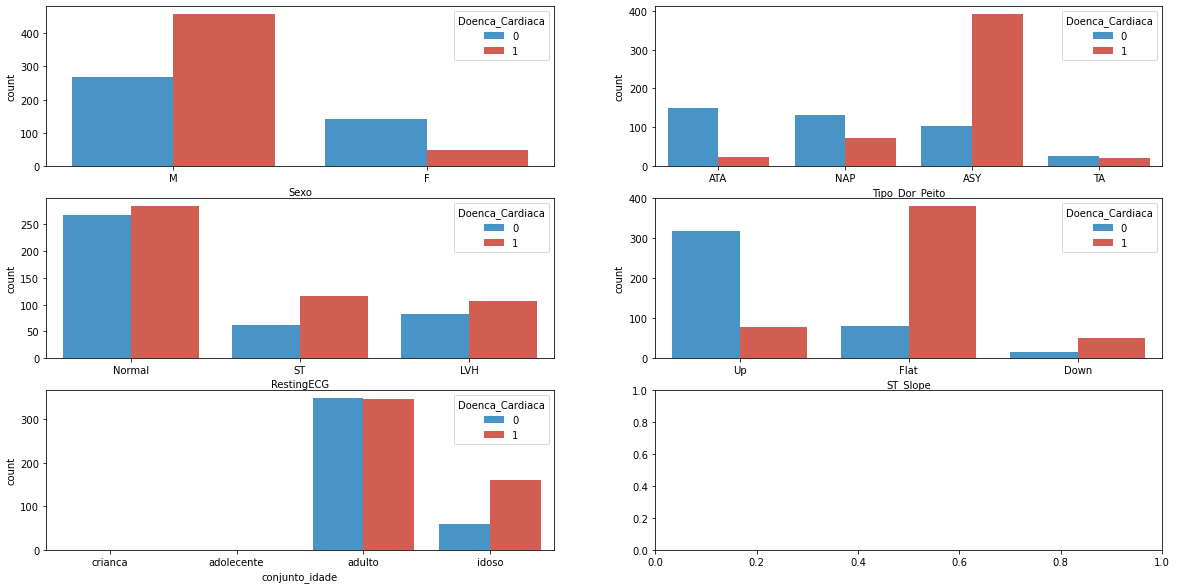
Grafico Sexo

odemos perceber que Homens tem maiores chances de ter Insuficiencia Cardíaca mesmo que tenham maior volume de dados. Já as Mulheres tem grandes chances de NÃO ter algum problema cardíaco. Nota-se que os valores de casos sem a doença chega a ser 3/4 do conjunto de Mulheres

Grafico Tipo de dor no peito

• TA: Angina Típica, ATA: Angina Atípica, NAP: Dor Não Anginosa, ASY: Assintomática

Nota-se que de toda a classe Tipo_Dor_Peito a que mais se destaca é o classificador ASY, que representa uma dor Assintomática, em outras palavras, uma dor com poucos sintomas, ou pouco visivel. Vemos que o risco de ter insuficiência cardíaca é extremamente alta contendo esse tipo de dor.

No tipo TA, mesmo tendo um pequeno volume de dados, percebe-se que a quantidade de casos com e sem insuficiência é quase balanceado. Para esses casos deve-se ter mais atenção na hora dos diagnósticos para que o paciente não seja classificado sem a doença cardíaca.

Devemos perceber que nos tipos NAP e ATA temos um menor volume de dados contendo Insuficiência Cardíaca comparado com ASY e TA.

RestingECG

• Resultados do eletrocardiograma de repouso [Normal: normal, ST: com anormalidade da onda ST-T (inversões da onda T e/ou elevação ou depressão do ST > 0,05 mV), HVE: mostrando provável ou definitiva hipertrofia ventricular esquerda pelos critérios de Estes]

dentifica-se que a maioria dos pacientes, independente do resultado do eletrocardiograma, possuem chances de ter algum problema cardíaco.

Grafico ST_Stope

• Exame de Teste de Esforço
• ST_Slope: inclinação do segmento ST do exercício de pico [Up: upsloping, Flat: flat, Down: downsloping]

Nos resultados do ST_Slope pessoas com segmento ST maiores(UP), não tendem a ter insuficiencia cardíaca, visto que os bastimentos estão com um BPM alto.

Se mesmo no Teste de esforço físico o segmento ST estiver sem muita variação(Flat), a tendência a ter insuficiência cardíaca é bem alta. A mesma coisa quando o segmento ST estiver baixo(Down).

Conjunto Idade

O conjunto de idade foi criado na parte de discretização justamente para categorizar cara pessoa por seu devido conjunto de idade sende eles:

• [Criança - 0 à 12
• [Adolecente] - 12 à 20
• [Adulto] - 20 à 60
• [Idoso] - 60 à 100

Como podemos perceber, no DataSet não ha nenhum registro de pessoas da categoria “Criança” e “Adolecente”. Nota-se que a 50% de de todos os Adultos tem alguma insuficiência cardíaca, e tambem cerca de 75% dos Idosos tambem foram diagnosticado com essa doença.

Iremos retirar a coluna de idade, visto que com a nova coluna de “conjunto_idade” poderemos utilizar facilmente no treinamento dos modelos.

heart_df.drop(columns=['Idade'], inplace=True)

Inicio de Treinamento de Modelos

Separação de Dados

Antes de começarmos a criar qualquer modelo, precisaremos separar os dados do Dataframe em dois grupos, um de Treino e outro de Teste.

• Dados de Treino Os dados de treino são responsáveis por serem as informações que o Algoritmo de Machine Learnig usara para a criação de um modelo. No nosso caso utilizamos 70% do DataSet para o treinamento.

• Dados de Teste Os dados de teste são aplicados ao modelo criado, simulando previsões reais que o modelo realizará, fazendo com que seja verificado o desempenho real do modelo. Utilizaremos 30% do DataSet para Teste.

• Separando dados de Treino e Teste para criação de modelos.

• Alterando o type das informações para ‘Category’.

y = heart_df['Doenca_Cardiaca'].values
heart_df.drop(columns=['Doenca_Cardiaca'], inplace=True)

X = heart_df

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0, stratify=y)

for c in X_test.columns:
    if type(X_test[c].iloc[0]) == str:
        X_test[c] = X_test[c].astype('category')
        X_test[c] = X_test[c].cat.codes
        
for c in X_train.columns:
    if type(X_train[c].iloc[0]) == str:
        X_train[c] = X_train[c].astype('category')
        X_train[c] = X_train[c].cat.codes

——– Desision Tree Train ——–

O algoritmo Árvore de Decisão pertence à família de algoritmos de aprendizado SUPERVISIONADO. Ao contrário de outros algoritmos de aprendizado supervisionado, o algoritmo de árvore de decisão também pode ser usado para resolver problemas de regressão e classificação . O objetivo de usar uma Árvore de Decisão é criar um modelo de treinamento que possa ser usado para prever a classe ou valor da variável de destino aprendendo regras de decisão simples inferidas de dados anteriores (dados de treinamento). Em Árvores de Decisão, para prever um rótulo de classe para um registro, começamos da raiz da árvore. Comparamos os valores do atributo root com o atributo do registro. Com base na comparação, seguimos o ramo correspondente a esse valor e saltamos para o próximo nó.

Medidas de seleção de atributo

Se o conjunto de dados consiste em N atributos, decidir qual atributo colocar na raiz ou em diferentes níveis da árvore como nós internos é uma etapa complicada. Apenas selecionar aleatoriamente qualquer nó para ser a raiz não pode resolver o problema. Se seguirmos uma abordagem aleatória, isso pode nos dar resultados ruins com baixa precisão.

Nesses cassos usamos alguns critérios para fazer calculos diferentes na hora da distribuição, sendo algum deles:

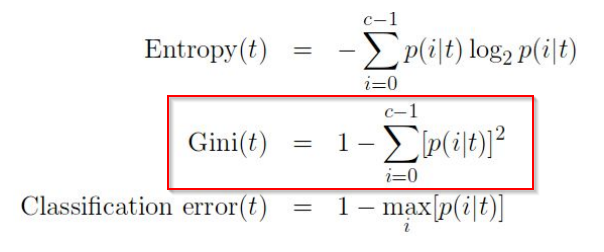
• p(i/t) –> peso = quantia de indice da classe/ quantia todal de indices

tree_view = DecisionTreeClassifier(criterion='gini',random_state=0, max_depth=4)

# .fit é o comando de treinamento(lembre de fitness. o que treina)
model = tree_view.fit(X_train, y_train)
prediction_tree_train = model.predict(X_train)
accuracy = accuracy_score(y_train, prediction_tree_train)
print('Valor Acuracia: ',accuracy)

Valor Acuracia: 0.881619937694704

——– Decision Tree Test ——–

tree_view_test = DecisionTreeClassifier(criterion='gini',random_state=0, max_depth=4)

prediction_tree_test = model.predict(X_test)
accuracy = accuracy_score(y_test, prediction_tree_test)
print('Valor Acuracia: ',accuracy)

Valor Acuracia: 0.8297101449275363

nome_features = X_test.columns

plt.figure(figsize=(24,11))

plt.title('teste')
tree.plot_tree(model, label=None, node_ids=True, rounded=True, fontsize=9, feature_names=nome_features, filled=True, class_names=['0','1'], proportion=True)
# plt.savefig('decision_tree.png', format='png')
plt.show()

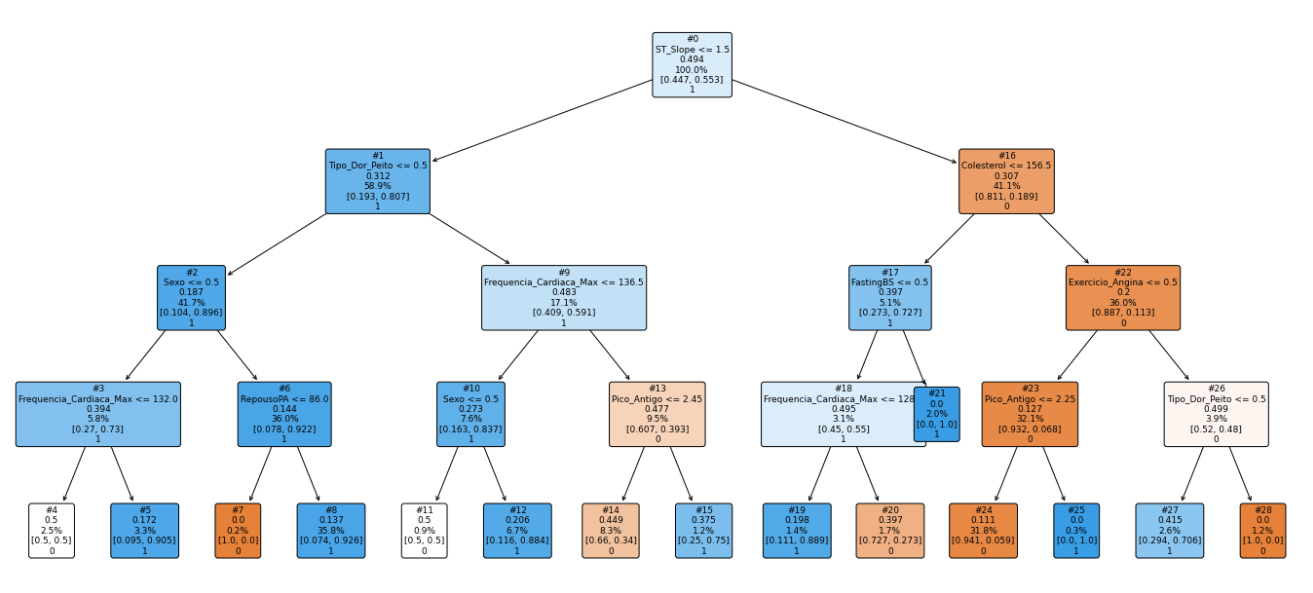
——– Randon Forest Train ——–

O algoritmo Random Forest é um tipo de ensemble learning, método que gera muitos classificadores e combina o seu resultado.

No caso do Random Forest, ele gera vários decision trees, cada um com suas particularidades e combinada o resultado da classificação de todos eles. Essa combinação de modelos, torna ele um algoritmo muito mais poderoso do que o Decision Tree

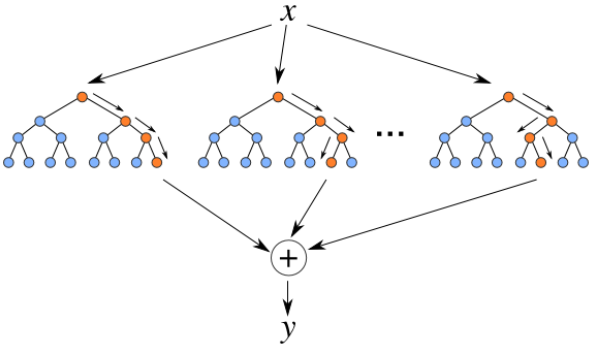
SEED=42
randon_forest = RandomForestClassifier(max_depth=5, random_state = SEED)

model_rando_forest = randon_forest.fit(X_train, y_train)
prediction_rf_train = model_rando_forest.predict(X_train)

accuracy = accuracy_score(y_train, prediction_rf_train)
print('Valor Acuracia: ',accuracy)

Valor Acuracia: 0.9003115264797508

——– Randon Rorest Test ——–

prediction_rf = model_rando_forest.predict(X_test)

accuracy = accuracy_score(y_test, prediction_rf)
print('Valor Acuracia: ',accuracy)

Valor Acuracia: 0.8623188405797102

——– Logistic Regression Train ——–

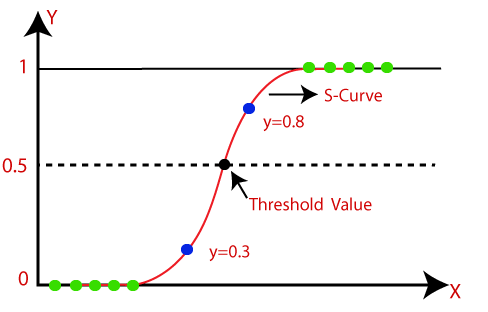
Regressão logística pode ser definido como uma técnica estatística que busca produzir (usando um conjunto de observações) um modelo que possibilita predizer os valores tomados por uma variável categórica.

Como no algoritmos da Regressão Logistica as variáveis são independentes, são analisados os resultados binários e sendo direcionada a uma das duas categorias. As variáveis independentes podem ser categóricas ou numéricas, mas a variável dependente é sempre categórica. Escrito assim:

P(Y=1|X) ou P(Y=0|X)

Isso pode ser usado para calcular a probabilidade de uma palavra ter uma conotação positiva ou negativa (0, 1 ou em uma escala intermediária). Ou pode ser usado para determinar o objeto contido em uma foto (árvore, flor, grama, etc.), com cada objeto dado uma probabilidade entre 0 e 1.

logistic_regression = LogisticRegression(max_iter = 1000 ,random_state = 0)
model_logistic_regression = logistic_regression.fit(X_train, y_train)
prediction_lr_train = model_logistic_regression.predict(X_train)

y_accuracy = accuracy_score(y_train, prediction_lr_train)
print("Acurácia:", y_accuracy)

Acurácia: 0.8411214953271028

——– Logistic Regression Test ——–

prediction_lr_test = model_logistic_regression.predict(X_test)
y_accuracy = accuracy_score(y_test, prediction_lr_test)
print("Acurácia:", y_accuracy)

Acurácia: 0.8405797101449275

——– GaussianNB Train ——–

O Teorema de Bayes é usada para o cálculo da probabilidade de um evento dado que outro evento já ocorreu, o que é chamado de probabilidade condicional.

A grande questão do Teorema de Bayes é que eu preciso ter alguma informação anterior, ou seja, preciso saber que um determinado evento já ocorreu e qual a probabilidade desse evento.

Calculo do algoritmo

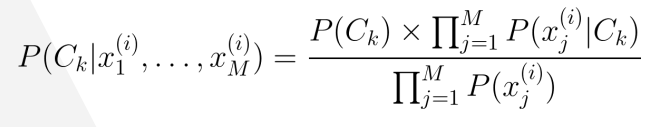
gnb = GaussianNB()
modelo_gaucianNB = gnb.fit(X_train, y_train)

preds_naivebaies_train = modelo_gaucianNB.predict(X_train)

y_accuracy = accuracy_score(y_train, preds_naivebaies_train)
print("Acurácia:", y_accuracy)

Acurácia: 0.8426791277258567

——– GaussianNB Train ——–

reds_naivebaies_teste = modelo_gaucianNB.predict(X_test)
y_accuracy = accuracy_score(y_test, reds_naivebaies_teste)
print("Acurácia:", y_accuracy)

Acurácia: 0.8333333333333334

Criação de objeto de classificadores

classifiers = {'Arvore': DecisionTreeClassifier(random_state=0, max_depth=4),
               'Random Forest': RandomForestClassifier(max_depth= 5, random_state = SEED),
               'Naive Bayes': GaussianNB(),
               'Regressão Logistica': LogisticRegression(max_iter = 1000 ,random_state = 0),
              }

for c in X_train.columns:
    if X_train[c].dtype == "object":
        X_train[c] = X_train[c].astype('category')
        X_train[c] = X_train[c].cat.codes  

for clf in classifiers.items():
    clf[1].fit(X_train, y_train)
    preds = clf[1].predict(X_test)
    score = accuracy_score(preds, y_test)
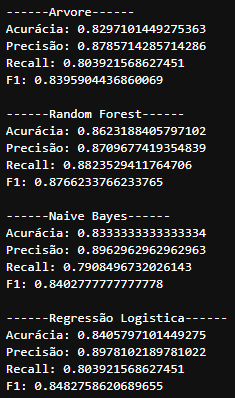
    print(f'\n------{clf[0]}------')
    print("Acurácia:",accuracy_score(y_test, preds))
    print("Precisão:",precision_score(y_test, preds))
    print("Recall:",recall_score(y_test, preds))
    print("F1:",f1_score(y_test, preds))

preds = []
clf_trained = []
names=[]
for clf in classifiers.items():
    clf_atual = clf[1].fit(X_train, y_train)
    clf_trained.append(clf_atual)

    pred_atual=clf[1].predict(X_test)
    preds.append(pred_atual)
    names.append(clf[0])
    
    print(precision_recall_fscore_support(y_test, pred_atual, average='macro'))

(0.8289915966386554, 0.832855093256815, 0.8290616311094128, None) (0.8611037056784858, 0.8598756575801052, 0.8604428358526719, None) (0.8346729708431836, 0.8385142674956161, 0.8330176767676768, None) (0.8409914404243028, 0.8450502152080345, 0.8401684653856278, None)

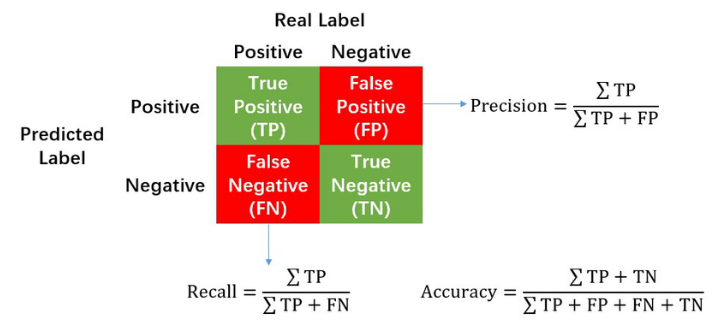
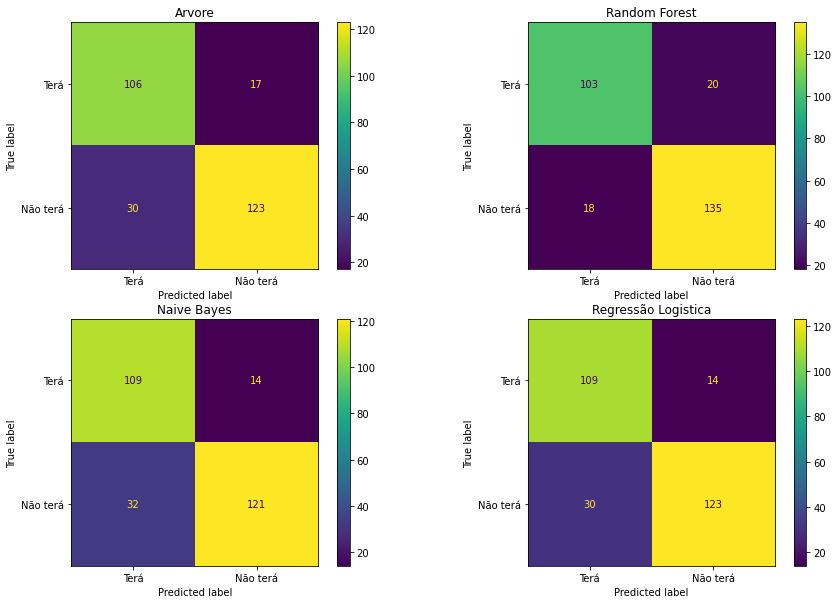
Matriz Confusão

fig, axs =  plt.subplots(2, 2, figsize=(15, 10))
position = [axs[0,0],axs[0,1],axs[1,0],axs[1,1]]

for i in range(len(classifiers)):
    cm = confusion_matrix(y_test, preds[i], labels=clf_trained[i].classes_)
    disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=["Terá", "Não terá"])
    position[i].set_title(names[i])
    disp.plot(ax=position[i])
    
plt.show()

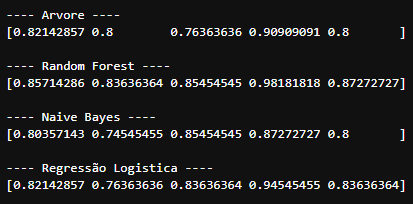
Cross-Validation

A escolha da validação cruzada correta depende do conjunto de dados com o qual você está lidando, e a escolha da validação cruzada em um conjunto de dados pode ou não se aplicar a outros conjuntos de dados. No entanto, existem alguns tipos de técnicas de validação cruzada que são as mais populares e amplamente utilizadas. Esses incluem:

• validação cruzada k-fold.
• validação cruzada estratificada em k-fold A validação cruzada é dividir os dados de treinamento em algumas partes. Treinamos o modelo em algumas dessas peças e testamos nas demais.

for i in classifiers.items():
    scores_dt = cross_val_score(i[1], X_test, y_test, scoring='accuracy', cv=5)
    print(f'\n---- {i[0]} ----')
    print(scores_dt)

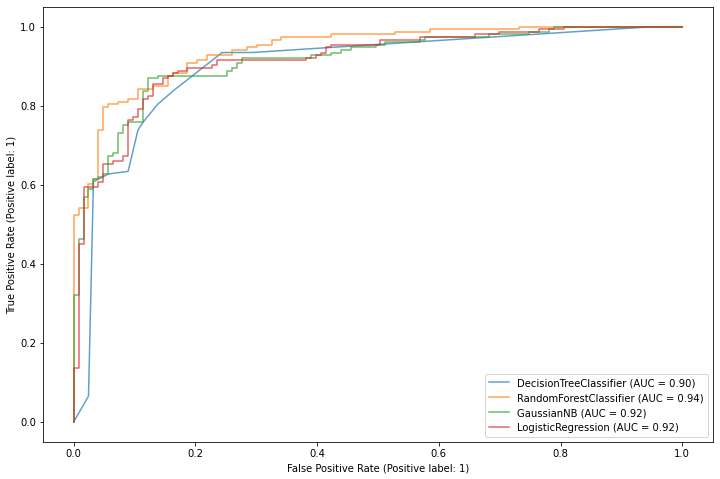
Curva ROC

ax = plt.gca()
for i in range(len(classifiers)):
    clf = classifiers[names[i]]      
    rfc_disp = RocCurveDisplay.from_estimator(clf, X_test, y_test, ax=ax, alpha=0.7)
plt.show()
    
clf2 = classifiers['Random Forest']
svc_disp = RocCurveDisplay.from_estimator(clf2, X_test, y_test)
svc_disp.plot(ax=ax, alpha=0.8)
plt.show()

Insigths

Após toda a análise do problema e entendimento de algumas hipóteses vistas na etapa de Visualização, criamos o conjunto de treino e testes e aplicamos em diferentes algoritmos. Iniciamos o treinamento dos algoritmos com a tradicional Decision Tree, partindo para Random Forest, GussianNB e Logistic Regression. Para a precisão dos resultados dos treinamentos, aplicamos uma camada de Cross-Validation onde os modelos passaram por diferentes conjuntos de dados, resultando em score variados para validarmos a qualidade dos modelos.

Após essa validação, identificamos que o modelo Random Forest se destacou com uma Acurácia media de 0.88 e uma derivação de 0.05, sendo o melhor resultado da acurácia de todos os algoritmos.

Como estamos predizendo um problema de saúde, devemos ter o seguinte pensamento: caso o paciente vá a um médico é melhor que ele seja diagnosticado com uma doença cardíaca e previna, porem ele NÃO tem nenhum problema. Do que ele seja diagnosticado que não tem uma doença cardíaca, e, na verdade, ele TEM problema cardíaco.

Logo, compreendemos que em nossos algoritmos devem conter um BAIXO índice de falsos negativos(FN). Analisando a matriz confusão, nota-se que dentre os quatro algoritmos, apenas um se destaca por conter poucos falsos negativos(FN), a Random Forest. Nota-se que enquanto os outros modelos chegam a 30 ou 32 FN, a Random Forest chega diminuir quase pela metade, chegando aos 18 FN.

Para compararmos as probabilidades de acerto desses Falsos Negativos, devemos olhar para o maior Score de Recall, e novamente a Random Fores se destaca com seus 0.88 de assertividade.

Com isso, entendemos que para predizermos a insuficiência cardíaca de um paciente, podemos utilizar nosso modelo treinado com Random Forest visto que comparamos os resultados de suas predições, e também testamos a qualidade do modelo comprovando a sua eficácia em seus resultados.

Espero que tenha aproveitado todo o desenvolvimento do projeto, e que sua leitura tenha agregado conhecimentos.